Unlocking the Power of the Weighted Average Method for Solving Nonlinear PDEs: Insights from the Burger-Fisher Equation

A study by Loyinmi et al. (2025) titled “Exploring the Efficacy of the Weighted Average Method for Solving Nonlinear Partial Differential Equations: A Study on the Burger-Fisher Equation” published in EDUCATUM Journal of Science, Mathematics, and Technology reveals that WAM provides a stable and accurate numerical approach for solving the Burger-Fisher equation, making it a valuable tool for researchers dealing with nonlinear PDEs.

“

The Weighted Average Method (WAM) is a stable, accurate, and reliable numerical approach for solving nonlinear partial differential equations. – Loyinmi et al. 2025

The study “Exploring the Efficacy of the Weighted Average Method for Solving Nonlinear Partial Differential Equations: A Study on the Burger-Fisher Equation” investigates the effectiveness of the Weighted Average Method (WAM) in solving the Burger-Fisher equation, a nonlinear partial differential equation (PDE) that plays a crucial role in fields such as fluid dynamics, population dynamics, and chemical kinetics. This equation integrates aspects of both the Burgers equation and Fisher equation, making it essential for modeling convection, diffusion, and reaction processes, particularly in phenomena like shock wave formation and turbulence.

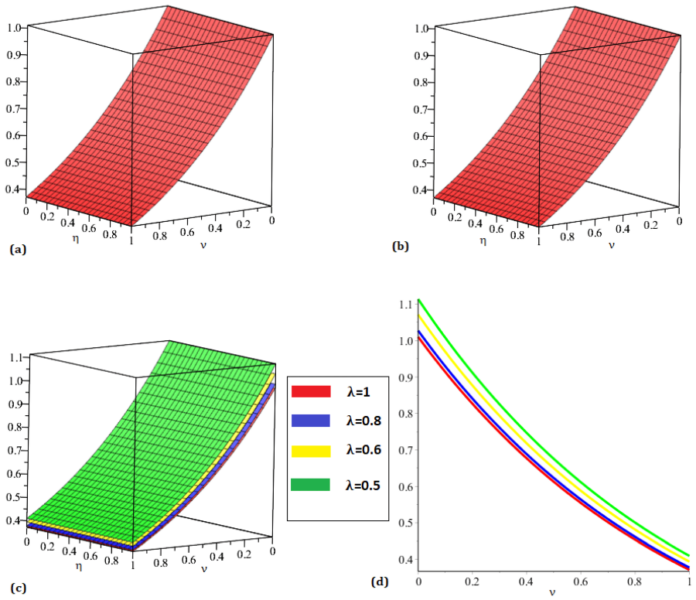
The Weighted Average Method discretizes spatial and temporal derivatives using a combination of forward, backward, and central differences. Its numerical implementation involves solving a tridiagonal matrix system at each time step, demanding substantial computational resources. To facilitate this, the study employs MATLAB and MAPLE for numerical computations. Comprehensive convergence and stability analyses validate the method’s reliability and accuracy, with comparisons against exact solutions revealing minimal errors, reinforcing the method’s effectiveness.

The findings demonstrate that WAM provides a stable and accurate numerical approach for solving the Burger-Fisher equation, making it a valuable tool for researchers dealing with nonlinear PDEs. The study underscores the importance of fine-tuning numerical parameters and leveraging computational techniques to enhance accuracy. Ultimately, this research contributes to the advancement of numerical methods, offering practical insights for solving complex mathematical models in various scientific and engineering applications.

How the Study was Conducted

The weighted average method discretizes both spatial and temporal derivatives using a combination of forward, backward, and central differences. The method’s implementation involves solving a tridiagonal matrix system at each time step, requiring significant computational resources. Mathematical software like MATLAB and MAPLE are utilized for computations. The convergence and stability analyses are conducted to ensure the method’s reliability and accuracy. The study compares numerical solutions obtained via the weighted average method with exact solutions, finding negligible errors that confirm the method’s accuracy.

What the Authors Found

The authors findings demonstrate that WAM is a highly accurate, stable, and practical numerical method for addressing complex nonlinear PDEs. These results have significant implications for scientific and engineering applications, offering a robust computational tool for solving challenging mathematical problems.

Why is this important?

Advancing Numerical Methods: The Weighted Average Method (WAM) is demonstrated to be highly accurate and reliable for solving nonlinear partial differential equations (PDEs), like the Burger-Fisher equation. This contributes to the advancement of numerical methods, providing researchers with a powerful tool for addressing complex mathematical problems.

Practical Applications: The Burger-Fisher equation models phenomena such as convection, diffusion, and reaction processes, which are fundamental in various scientific disciplines like fluid dynamics, population dynamics, and chemical kinetics. The ability to solve this equation accurately has practical implications in these fields, aiding in the development of predictive models and enhancing our understanding of these processes.

Improving Computational Techniques: By utilizing mathematical software like MATLAB and MAPLE to implement the Weighted Average Method, the study highlights the importance of leveraging computational resources. This approach ensures high accuracy and stability in solving nonlinear PDEs, which is essential for practical applications and further research.

Cross-Disciplinary Relevance: The study’s findings are not limited to the Burger-Fisher equation alone but have broader implications for other nonlinear PDEs encountered in diverse scientific and engineering fields. The principles and methodologies developed in this research can be applied to a wide range of problems, making the study valuable across multiple disciplines.

Improving Accuracy in Predictions: Accurate numerical solutions to nonlinear PDEs, like those provided by the Weighted Average Method, are crucial for developing reliable predictive models. These models are essential for understanding and forecasting behaviors in complex systems, from fluid flow and heat transfer to biological processes and chemical reactions.

Foundation for Further Studies: The study’s rigorous analysis of stability and convergence, as well as its demonstration of the practical utility of the Weighted Average Method, provides a solid foundation for future research. Researchers can build on these findings to develop even more efficient and accurate numerical methods for solving nonlinear PDEs.

What the Authors Recommended

Based on the finding, the authors recommend the following:

• Parameter Optimization: Researchers should focus on fine-tuning numerical parameters, such as the time step size (Δ𝑡) and spatial step size (Δ𝑥), to achieve optimal accuracy when using the Weighted Average Method (WAM) for solving nonlinear PDEs like the Burger-Fisher equation.
• Computational Resources: The study emphasizes the importance of leveraging computational resources effectively. Utilizing mathematical software like MATLAB and MAPLE can help manage the computational demands of solving the tridiagonal matrix system at each time step.
• Application to Other Nonlinear PDEs: The authors suggest that the Weighted Average Method, demonstrated to be effective for the Burger-Fisher equation, could be applied to other nonlinear partial differential equations. This can further validate the method’s robustness and versatility across different scientific and engineering fields.
• Further Research: The study encourages future research to build on their findings by exploring the application of WAM to more complex and higher-dimensional nonlinear PDEs. This could expand the method’s applicability and contribute to the development of more advanced numerical techniques.
• Practical Implementations: Practitioners and researchers are encouraged to use the Weighted Average Method for practical applications in fields such as fluid dynamics, population dynamics, and reaction-diffusion systems. The method’s high accuracy and stability make it a valuable tool for developing reliable predictive models.
• Stability and Convergence Analyses: The authors recommend conducting thorough stability and convergence analyses for any numerical method applied to nonlinear PDEs. Ensuring the method’s reliability through these analyses is crucial for achieving precise numerical approximations.

In conclusion, the study by Loyinmi et al. (2025) highlights the effectiveness of the Weighted Average Method (WAM) as a stable and accurate numerical approach for solving nonlinear partial differential equations like the Burger-Fisher equation. By leveraging advanced computational tools such as MATLAB and MAPLE, the research underscores the importance of optimizing numerical parameters and conducting rigorous stability and convergence analyses. The findings not only contribute to the advancement of numerical methods but also have far-reaching implications across various scientific and engineering disciplines, from fluid dynamics to chemical kinetics. As researchers continue to refine and expand the applications of WAM, this study serves as a valuable foundation for future developments in computational mathematics and predictive modeling.

AR Managing Editor (2025). Unlocking the Power of the Weighted Average Method for Solving Nonlinear PDEs: Insights from the Burger-Fisher Equation. Retrieved from https://www.africanresearchers.org/unlocking-the-power-of-the-weighted-average-method-for-solving-nonlinear-pdes-insights-from-the-burger-fisher-equation/